バルサラの破産確率とは、ナウザー・バルサラさんという数学者が
考案した、トレードを繰り返して資金が底をつく確率になります。
参考記事
この記事の中で、リスクリワードと勝率のバランスが大切だ!
と言うことを述べたのですが、今回はより具体的なお話です。
損益分岐点(プラスマイナスゼロ)だけで考えると
このようになります。
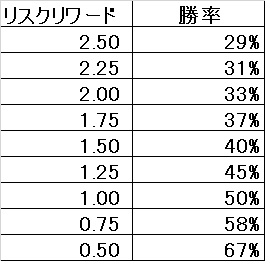
リスクリワードが、”2.0”あれば、
勝率は、33%以上であれば勝てる
逆に
リスクリワードが、”0.5”しかなければ、
勝率は、67%以上ないと勝てない
ということになります。
しかし、これがどのくらい破産する確率があるか?
そこで有名なのが【バルサラの破産確率】になります。
このバルサラの破産確率は、資産率によって変動します。
仮に1回のトレードに資金の10%を投入した場合、
(例:100万円の資金→1トレードに10万円を投入する。)
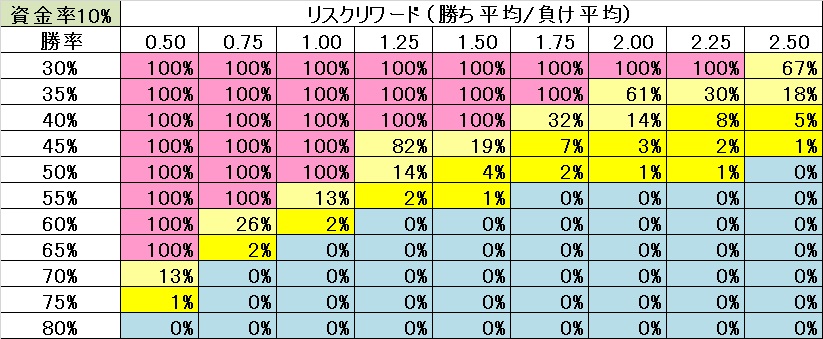
この表によると、先ほどの
リスクリワード(ペイオフレシオ)が、2.0なら
勝率33%で、トントンになるということですが、
破産する確率をゼロにするには、
勝率が55%以上必要になると言うことになります。
そして、
リスクリワード(ペイオフレシオ)が、0.5なら
勝率67%で、トントンになるということですが、
破産する確率をゼロにするには、
勝率が80%以上必要になると言うことになります。
ちなみにこの表だと、
リスクリワードが、1(勝ちも負けも同じ)場合、
トントンになるには、勝率50%ですが、
破産する確率をゼロにするには、
勝率が65%以上必要になると言うことになります。
つまり1回のトレードで資金10%を投入する場合、
勝率やリスクリワードに関係なく、かなり破産してしまう確率が高い
ということが言えます。
次に1回のトレードに資金の5%を投入した場合、
(例:100万円の資金→1トレードに5万円を投入する。)
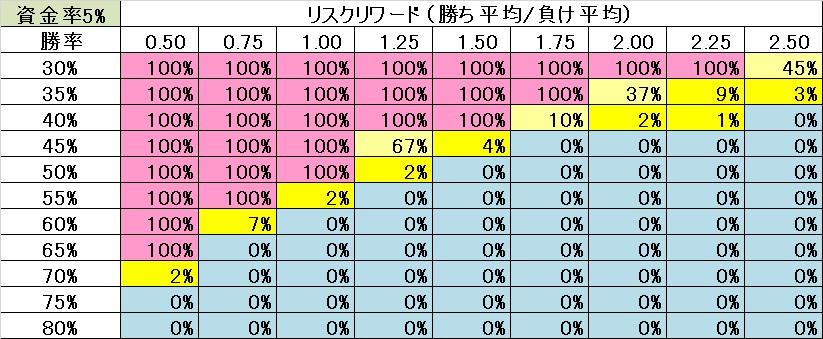
この表によると、先ほどの
リスクリワード(ペイオフレシオ)が、2.0なら
勝率33%で、トントンになるということですが、
破産する確率をゼロにするには、
勝率が45%以上必要になると言うことになります。
そして、
リスクリワード(ペイオフレシオ)が、0.5なら
勝率67%で、トントンになるということですが、
破産する確率をゼロにするには、
勝率が75%以上必要になると言うことになります。
ちなみにこの表だと、
リスクリワードが、1(勝ちも負けも同じ)場合、
トントンになるには、勝率50%ですが、
破産する確率をゼロにするには、
勝率が60%以上必要になると言うことになります。
つまり1回のトレードで資金10%を投入する場合と比較し、
資金5%を投入する場合、かなり破産率が下がると言えます。
(”1回のトレードに投入する金額を下げると破産しづらくなる”と言える)
そしてリスクリワードが低い(例:リスクリワード0.5)と
勝率が75%以上ないと破産する可能性があり、
そしてリスクリワードが高い(例:リスクリワード2.0)と
勝率が45%以上で破産する可能性がなくなるので、
俗世間的に言う”損小利大”だと相場で生き残れる確率が高くなる。
ということが言えます。
まー我々は、数学者ではないので、何が正しい理論なのか?
それを追求するよりも
リスクリワードと勝率のバランスが大切であること
そして、どのくらいの状態であれば、破産確率を低く出来るか
ということを理解しておけばよいと思います。
※ 何が正しい理論か? 知りたい方は、
こちらの文献がオススメです。